本文旨在探讨函数 y = Asin(ωx+φ) 的图像及其性质
函数 图像与性质
教学目标
- 结合具体实例,解释 y=A sin(ωx+φ) 的实际意义。
- 能利用 的图像理解参数 、、 的意义,了解参数的变化对图像的影响,掌握 与 图像之间的变换关系,并能正确地指出其变换步骤。
- 会用“五点法”画出函数 的图像,并能通过 的图像确定其解析式。
教学重点、难点
- 重点:用“五点法”讨论函数 的图像变换过程。
- 难点:图像变换与函数解析式变换的内在联系。
一、复习旧知
复习 、、 的图像及性质。
函数
| 函数 | | | |
|---|
| 图像 | 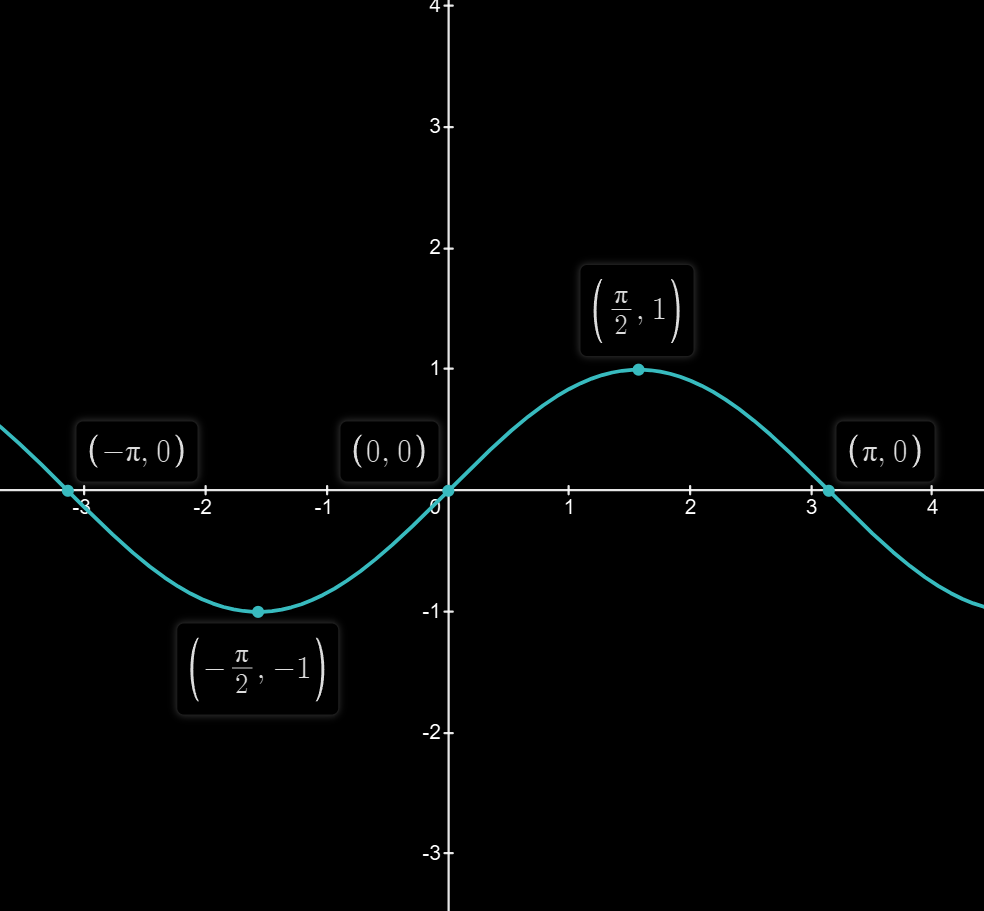 | 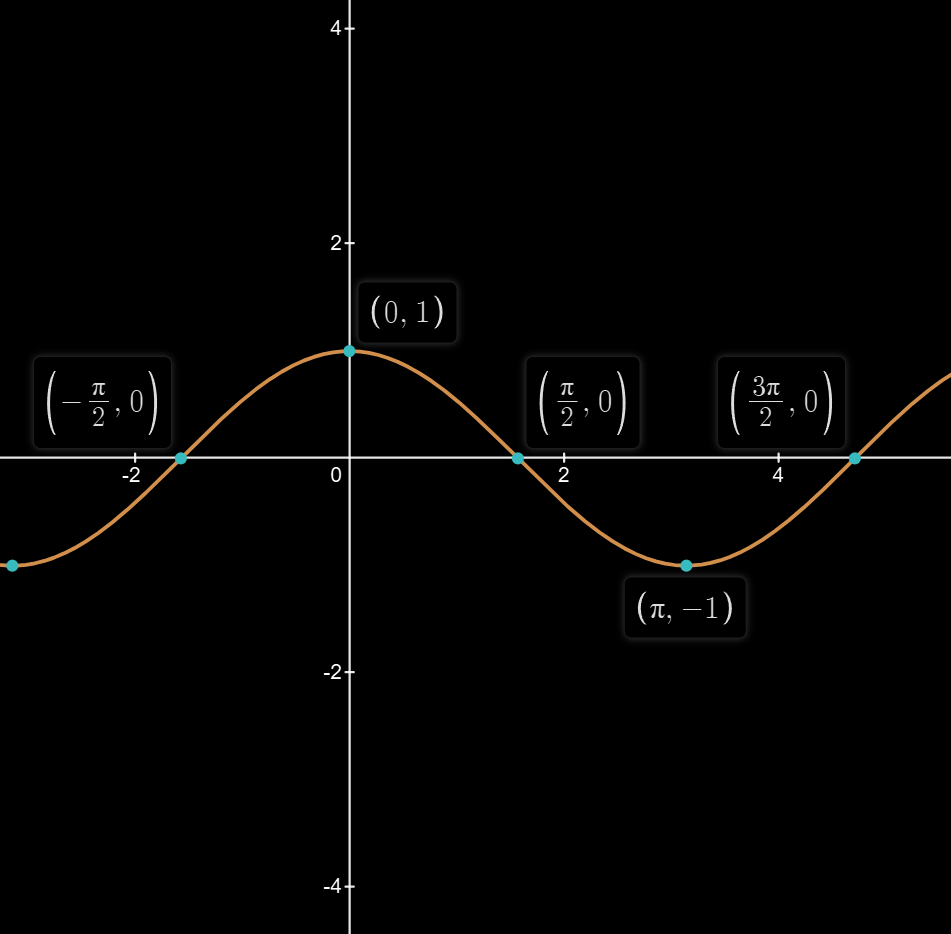 | 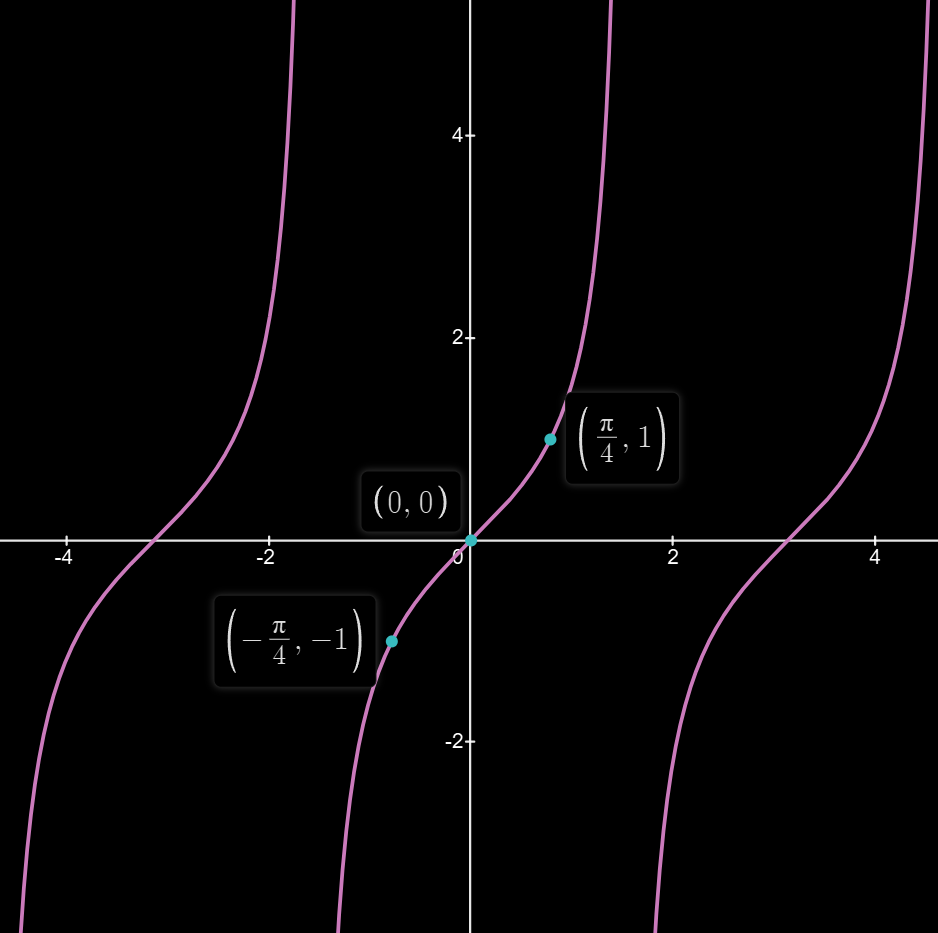 |
| 作图 | | | |
| 定义域 | | | |
| 值域 | | | |
| 奇偶性 | 奇 | 偶 | 奇 |
| 周期性 | | | |
| 单调性 | 增
减 | 减
增 | 增
减 |
| 最值 |
|
| 无 |
函数图像生成网站